Does P equals NP? after “how humans evolved”, this is the biggest ques, Darwin of which is yet to be discovered.
Welcome. Take a seat. We have been awaiting your arrival for quite a long time. We are presenting you with an opportunity of a lifetime, an option that may completely change your life. Not only are we tempting your inner avarice by providing you with a chance to win a million dollars from the Clay Mathematics Institute, but also letting you know that if you solve this problem:
- Cancer diseases will be gone forever.
- Databases, scheduling, transportation systems will work at >never before achievable speeds.
- The biggest bait of all is that you can crack 10700 levels of Candy Crush with ease and can become the Universe boss.
This doesn’t end here; there are more spellbinding tasks that can bring an updated version of Earth. I am incredibly sorry if your business entirely depends on crypto-related algorithms as, if somehow someone someday shows P=NP, then the whole subject of cryptography has to be altered. Though we may have to dig for new privacy-keeping algorithms, I think it would still be worth it if P=NP.
Let’s dig a bit deeper into this. P is a class of problems that the human race has solved quickly and efficiently; by being “efficient”, I mean algorithms of these problems can be computed in polynomial time. ‘Polynomial time’ implies that the relation between time taken by computer and input size is a polynomial(also note P for polynomial). There’s another class of problems, known as NP, solutions of which humans can verify “efficiently” but can’t devise quick methods to solve. That is time that existing algorithms take eventually break the patience of not only humans but also of the Universe. That is, the time required by some of these algorithms is estimated to be more than the life of the Universe. For instance, say Sudoku, we can easily and quickly verify if all the rules hold in a given Sudoku puzzle but apparently, we can’t propose an algorithm that can solve any random puzzle in seconds.
Originally, NP was thought of as a much more extensive class of problems but was later divided into two subclasses. One of them consists of problems that some enthusiastic geeks, like our blog readers, get motivated and solved efficiently. While the bigger fish is NP-Complete problems that were initialized half a century ago by Stephen Cook, no one is yet able to find an efficient solution of the same. Even if one problem gets solved in polynomial time among these NP-Complete(also known as co-NP) problems, it can be said NP=P. Also, please do note, we are sure that P is contained in NP, as problems getting solved in polynomial time(P problems) also indicate that their solutions can be verified in polynomial time(NP problems). Broadly speaking, we have four options available to consider:
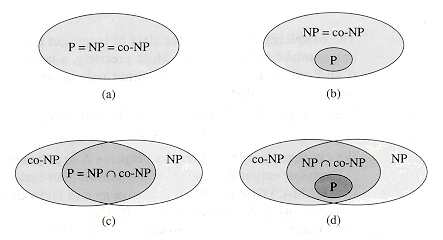
Bitterly saying, most theoretical Computer Scientists believe that NP doesn’t equal P. Delightfully typing, they haven’t got proof of this statement. Let’s look into some of the best attempts to prove P$\ne$NP of history.
Razborov’s “almost” Robust attempt
It has been proved that small circuits cannot solve the parity function if the circuits have a fixed number of layers of gates. Razborov showed the NP-complete problem of finding a large clique that does not have small circuits if one only allows AND and OR gates (no NOT gates). If one extends Razborov’s result to general circuits, one would have proved P doesn’t equal NP, however later, Roborov himself disagreed with previous results if NOT gate is also considered.
Daring Diagonalisation
This famous technique in mathematics was first used by Cantor to prove real numbers are uncountable. In his seminal paper on computation, Turing used a similar technique to show that the Halting problem is not computable. Therefore, theoretical experts tried this approach in an attempt to separate NP from P; some of them even got some fruitful results but weren’t able to satisfactorily prove P doesn’t equal NP.
Are you ready to undertake the challenge of delving further into this predicament? Check out Razborov’s attempt in more detail, and check out a deeper description of diagonalization.
[Image taken from http://staff.ustc.edu.cn/~csli/graduate/algorithms/book6/chap36.htm]